Opened 7 years ago
Last modified 4 years ago
#5452 reopened defect
Numerical issues due to missing index reduction
| Reported by: | Francesco Casella | Owned by: | Karim Adbdelhak |
|---|---|---|---|
| Priority: | blocker | Milestone: | 1.19.0 |
| Component: | Backend | Version: | |
| Keywords: | Cc: | Karim Adbdelhak, Lennart Ochel, Volker Waurich, dr.christian.kral@…, a.haumer@… |
Description
Please consider the results of the simulation of Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive.
The initialization terminates correctly, but when the simulation starts, the step length is reduced down to 7e-15, and then the simulation fails. It looks like the DAE system is somewhat singular (e.g., locally index 2), in the sense that all state derivatives cannot be uniquely computed at the beginning of the state-space simulator. The same behviour takes place with the old front-end.
The exact reason of this singularity is yet unknown, it should be analyzed and then fixed.
Attachments (12)
Change History (68)
comment:1 by , 7 years ago
| Priority: | high → blocker |
|---|
comment:2 by , 7 years ago
| Resolution: | → fixed |
|---|---|
| Status: | new → closed |
Try to get 100% of MSL to work in 1.14.0
comment:3 by , 7 years ago
| Resolution: | fixed |
|---|---|
| Status: | closed → reopened |
comment:4 by , 7 years ago
| Owner: | changed from to |
|---|---|
| Status: | reopened → assigned |
comment:5 by , 7 years ago
For the initialization problem OMC converges to a different solution than Dymola for the non-linear loop
LOG_NLS_V | info | solution for NLS 302 at t=0 | | | | | [1] inverter.dc_n.v = 1638.56 | | | | | [2] rectifier.diode_n.idealDiode[1].s = -270.095 | | | | | [3] rectifier.diode_p.idealDiode[1].s = -270.095 | | | | | [4] inverter.diode_n.idealDiode[1].s = -1.08038e-07 | | | | | [5] rectifier.diode_n.idealDiode[2].s = -270.095 | | | | | [6] rectifier.diode_p.idealDiode[2].s = -270.095 | | | | | [7] rectifier.diode_p.idealDiode[3].s = -270.095 | | | | | [8] rectifier.diode_n.idealDiode[3].s = -270.095 | | | | | [9] inverter.transistor_p.idealGTOThyristor[1].s = 540.19 | | | | | [10] inverter.transistor_p.idealGTOThyristor[2].s = 540.19 | | | | | [11] inverter.diode_n.idealDiode[2].s = -1.08038e-07 | | | | | [12] inverter.diode_p.idealDiode[2].s = -540.19 | | | | | [13] inverter.transistor_n.idealGTOThyristor[2].s = 0.0108038 | | | | | [14] inverter.diode_p.idealDiode[3].s = -540.19 | | | | | [15] inverter.transistor_p.idealGTOThyristor[3].s = 540.19 | | | | | [16] inverter.transistor_n.idealGTOThyristor[3].s = 0.0108038 | | | | | [17] inverter.diode_n.idealDiode[3].s = -1.08038e-07 | | | | | [18] inverter.transistor_n.idealGTOThyristor[1].s = 0.0108038 | | | | | [19] inverter.diode_p.idealDiode[1].s = -540.19
E.g Dymola says inverter.dc_n.v = -270.095 V Is 1600V even a reasonable solution?
Dymola finds 11 continuous time states, but modelica finds 12. Whats the reason for that?
comment:6 by , 7 years ago
| Cc: | added |
|---|---|
| Summary: | Numerical issues with the simulation of asynchronous machines. → Numerical issues due to missing index reduction |
Andreas, Karim, Lennart,
I compared the outcome with OMC with the Dymola output more closely. I think I have identified the root cause, which is an index reduction problem.
Dymola correctly selects inductor.inductor[2].i,inductor.inductor[3].i as states, while OMC also selects inductor.inductor[1].i. In fact, while analyzing the model, Dymola reports
Differentiated the equation inverter.ac.pin[1].i + inverter.ac.pin[2].i + inverter.ac.pin[3].i + inductor.inductor[1].i + inductor.inductor[2].i + inductor.inductor[3].i = 0.0; giving der(inverter.ac.pin[1].i) + der(inverter.ac.pin[2].i) + der(inverter.ac.pin[3].i) + der(inductor.inductor[1].i) + der(inductor.inductor[2].i) = -der(inductor.inductor[3].i);
This is very commonplace in 3-phase motor circuits, where you have three inductors (whose currents are potential states) connected in a star configuration, so that there are only two independend currents, hence only two states after index reduction.
Apparently, for some reasons OMC fails to recognize this, and then ends up with a high-index DAE that DASSL cannot solve, even by reducing the step to very tiny values.
The reason of the weird initial solution is that OMC thinks there are 12 states, not 11, so it adds one more initial equation
[3] 13:53:51 Translation Warning
Assuming fixed start value for the following 1 variables:
inductor.inductor[3].i:VARIABLE(start = 0.0 unit = "A" )
"Current flowing from pin p to pin n"
Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive,
Modelica.Electrical.MultiPhase.Basic.Inductor,
Modelica.Electrical.Analog.Basic.Inductor type: Real [3]
which is totally bogus and ends up with an unreasonably difficult initialization problem with 19 tearing variables. In fact, the correct initialization problem reported by Dymola only has a linear system of two equations, everything else is just plain assignments.
This should definitely be investigated with high priority.
comment:7 by , 7 years ago
| Cc: | added |
|---|
comment:8 by , 7 years ago
@Karim, I carried out some more analysis. When translating the model, Dymola reports differentiating the following equations constraining differentiated variables:
inductor.inductor[1].i+inductor.inductor[2].i+inductor.inductor[3].i = 0.0;
This equation obviously makes it impossible to have all the three inductor currents as states, as OMC does - doing so results in an index-2 problem, which eventually leads DASSL to fail. Unfortunately, Dymola will not tell me where it got those equations from.
Those equations do not show up directly in the flat model, so they must be obtained by the back-end after some manipulation. In fact, if you look at the model, the inductor component contains an array of 3 inductors, each with and equation containing der(i), but then the constraint on the sum of the three currents to be zero is obviously found somewhere else, so it doesn't involve directly the variables of the inductor.
Now, for simpler circuits such as the one in the attached TestIndexReduction.mo, OMC somehow manages to figure out that constraint, and comes up with an index-1 DAE that only has two of the three inductor currents as states. I have no idea how it does, but you can check that out in that much simpler model (only 200 equations instead of 5000). If you can then explain it to me, I would be grateful :)
I guess the trouble comes from the rectifier/inverter circuits, possibly because they have conditional expressions. Eventually, the sum of the currents in the three-phases of those components is still zero, but it seems that the back-end cannot figure that out.
If you try out the attached TestIndexReduction2.mo model, that also contains the diode-based circuits, OMC crashes (!). However, when I tried to understand where that happened by setting -d=exectstat, it actually built the code (we should understand why this happens, BTW, maybe this is also a tell-tale sign of issues in the index reduction algorithm). Then, the simulation failed for the usual reason, and indeed all three inductor currents were present in the state selection. Apparently, the presence of the diode equations prevents the back-end to figure out that a constraint among the three inductor currents exists, as all other equations involving currents are simple linear equations as the ones found in the previous example.
I think you should be able to understand the problem and fix it by first understanding how index reduction works in the first case, and then why it doesn't in the second one. I'm sorry I couldn't come up with simpler test cases, but at least I managed to get rid of the asynchronous induction machine model, which makes the system model one order of magnitude smaller.
Good luck!
by , 7 years ago
| Attachment: | TestIndexReduction.mo added |
|---|
by , 7 years ago
| Attachment: | TestIndexReduction2.mo added |
|---|
comment:9 by , 7 years ago
| Cc: | added |
|---|---|
| Owner: | changed from to |
@dr.christian.kral, we are trying to fix some remaining issues with OMC and electrical machine models in the MSL. I would be grateful if you could give a look at this ticket and help us with this, because I am not too familiar with the structure of the involved models, particularly the asynchronous motor model.
Specifically, I have a two questions
- Regarding the original model in the MSL, I really couldn't figure out exactly where Dymola gets the constraint equation
inductor.inductor[1].i+inductor.inductor[2].i+inductor.inductor[3].i = 0.0;. I tried to follow the current flows from the three-phase star-connected sources, through the line, rectifier, inverter, and machine, and as far as I understood the sum of the three currents is eventually going into thelszeroinductor, which is connected to ground, so it is not necessarily zero. It turns out to be so because the three voltage sources are balanced and the whole circuit is, but if there was a zero-sequence component in the source voltages,that current would be non-zero. Do I miss something? Where does Dymola take that constraint equation from? - I tried to reproduce the index reduction issue without the machine model (see the two attached models), terminating the circuit with a star connection and inductor connected to the starpoint that should somehow replicate the role of
lszero, but in these cases the constraint equation Dymola differentiated wasinductor.inductor[1].i+inductor.inductor[2].i+inductor.inductor[3].i- inductor1.i = 0.0;. Why is this case different from the MSL test case?
Thank you!
comment:10 by , 7 years ago
I updated the -d=bltdump of omc, it has just been added to the trunk. I can provide the information it dumps for the original model of the inverter drive. It is quite large but i added some commentary.
The first information is from the matching algorithm regarding minimal structurally singular subsets (MSSS). Since everything differs from the information dymola outputs, the error might have already happened before.
unmatched equations: 172, 176, 216, 218, 222, 224, 227, 228, 230 Index Reduction neccessary! MSS subsets: 218, 229, 220, 226, 223, 225, 221, 222, 224, 227, 228, 230, 219 216 176 172
Following information is a summary of all MSSS and the constraint equations that get differentiated.
##############--MSSS--############## Indices of constraint equations:172 ------------------172------------------ Constraint equation to be differentiated: aimc.phiMechanical = loadTorque.phi - aimc.fixed.phi0 Differentiated equation: aimc.wMechanical = loadInertia.w Update Incidence Matrix: 172 ##############--MSSS--############## Indices of constraint equations:176 ------------------176------------------ Constraint equation to be differentiated: aimc.friction.phi = loadTorque.phi - aimc.fixed.phi0 Differentiated equation: aimc.friction.w = loadInertia.w Update Incidence Matrix: 176 ##############--MSSS--############## Indices of constraint equations:216 ------------------216------------------ Constraint equation to be differentiated: aimc.strayLoad.phi = loadTorque.phi - aimc.fixed.phi0 Differentiated equation: aimc.strayLoad.w = loadInertia.w Update Incidence Matrix: 216https://github.com/OpenModelica/OpenModelica/pull/270 ##############--MSSS--############## Indices of constraint equations:218 229 220 226 223 225 221 222 224 227 228 230 219 ------------------219------------------ Constraint equation to be differentiated: aimc.airGapS.i_ms[2] = aimc.lssigma.i_[2] + aimc.idq_rs[2] Differentiated equation: der(aimc.airGapS.i_ms[2]) = der(aimc.lssigma.i_[2]) + der(aimc.idq_rs[2]) ------------------230------------------ Constraint equation to be differentiated: aimc.idq_rs[2] = aimc.airGapS.RotationMatrix[2,1] * aimc.idq_rr[1] + aimc.airGapS.RotationMatrix[2,2] * aimc.idq_rr[2] Differentiated equation: der(aimc.idq_rs[2]) = aimc.airGapS.RotationMatrix[2,1] * der(aimc.idq_rr[1]) + der(aimc.airGapS.RotationMatrix[2,1]) * aimc.idq_rr[1] + aimc.airGapS.RotationMatrix[2,2] * der(aimc.idq_rr[2]) + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.idq_rr[2] ------------------228------------------ Constraint equation to be differentiated: aimc.lssigma.i_[2] = aimc.airGapS.RotationMatrix[2,1] * aimc.idq_sr[1] + aimc.airGapS.RotationMatrix[2,2] * aimc.idq_sr[2] Differentiated equation: der(aimc.lssigma.i_[2]) = aimc.airGapS.RotationMatrix[2,1] * der(aimc.idq_sr[1]) + der(aimc.airGapS.RotationMatrix[2,1]) * aimc.idq_sr[1] + aimc.airGapS.RotationMatrix[2,2] * der(aimc.idq_sr[2]) + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.idq_sr[2] ------------------227------------------ Constraint equation to be differentiated: aimc.lssigma.i_[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.idq_sr[1] - aimc.airGapS.RotationMatrix[2,1] * aimc.idq_sr[2] Differentiated equation: der(aimc.lssigma.i_[1]) = aimc.airGapS.RotationMatrix[2,2] * der(aimc.idq_sr[1]) + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.idq_sr[1] + (-aimc.airGapS.RotationMatrix[2,1]) * der(aimc.idq_sr[2]) - der(aimc.airGapS.RotationMatrix[2,1]) * aimc.idq_sr[2] ------------------224------------------ Constraint equation to be differentiated: aimc.airGapS.gamma = /*Real*/(aimc.airGapS.p) * (loadTorque.phi - aimc.fixed.phi0) Differentiated equation: der(aimc.airGapS.gamma) = /*Real*/(aimc.airGapS.p) * loadInertia.w ------------------222------------------ Constraint equation to be differentiated: aimc.airGapS.psi_mr[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.psi_ms[1] + aimc.airGapS.RotationMatrix[2,1] * aimc.airGapS.psi_ms[2] Differentiated equation: aimc.airGapS.spacePhasor_r.v_[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.spacePhasor_s.v_[1] + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.airGapS.psi_ms[1] + aimc.airGapS.RotationMatrix[2,1] * aimc.airGapS.spacePhasor_s.v_[2] + der(aimc.airGapS.RotationMatrix[2,1]) * aimc.airGapS.psi_ms[2] ------------------221------------------ Constraint equation to be differentiated: aimc.airGapS.psi_ms[2] = aimc.airGapS.L[2,1] * aimc.airGapS.i_ms[1] + aimc.airGapS.L[2,2] * aimc.airGapS.i_ms[2] Differentiated equation: aimc.airGapS.spacePhasor_s.v_[2] = aimc.airGapS.L[2,1] * der(aimc.airGapS.i_ms[1]) + aimc.airGapS.L[2,2] * der(aimc.airGapS.i_ms[2]) ------------------225------------------ Constraint equation to be differentiated: aimc.airGapS.RotationMatrix[2,2] = cos(aimc.airGapS.gamma) Differentiated equation: der(aimc.airGapS.RotationMatrix[2,2]) = (-sin(aimc.airGapS.gamma)) * der(aimc.airGapS.gamma) ------------------223------------------ Constraint equation to be differentiated: aimc.airGapS.psi_mr[2] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.psi_ms[2] - aimc.airGapS.RotationMatrix[2,1] * aimc.airGapS.psi_ms[1] Differentiated equation: aimc.airGapS.spacePhasor_r.v_[2] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.spacePhasor_s.v_[2] + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.airGapS.psi_ms[2] + (-aimc.airGapS.RotationMatrix[2,1]) * aimc.airGapS.spacePhasor_s.v_[1] - der(aimc.airGapS.RotationMatrix[2,1]) * aimc.airGapS.psi_ms[1] ------------------226------------------ Constraint equation to be differentiated: -aimc.airGapS.RotationMatrix[2,1] = -sin(aimc.airGapS.gamma) Differentiated equation: -der(aimc.airGapS.RotationMatrix[2,1]) = (-cos(aimc.airGapS.gamma)) * der(aimc.airGapS.gamma) ------------------220------------------ Constraint equation to be differentiated: aimc.airGapS.psi_ms[1] = aimc.airGapS.L[1,1] * aimc.airGapS.i_ms[1] + aimc.airGapS.L[1,2] * aimc.airGapS.i_ms[2] Differentiated equation: aimc.airGapS.spacePhasor_s.v_[1] = aimc.airGapS.L[1,1] * der(aimc.airGapS.i_ms[1]) + aimc.airGapS.L[1,2] * der(aimc.airGapS.i_ms[2]) ------------------229------------------ Constraint equation to be differentiated: aimc.idq_rs[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.idq_rr[1] - aimc.airGapS.RotationMatrix[2,1] * aimc.idq_rr[2] Differentiated equation: der(aimc.idq_rs[1]) = aimc.airGapS.RotationMatrix[2,2] * der(aimc.idq_rr[1]) + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.idq_rr[1] + (-aimc.airGapS.RotationMatrix[2,1]) * der(aimc.idq_rr[2]) - der(aimc.airGapS.RotationMatrix[2,1]) * aimc.idq_rr[2] ------------------218------------------ Constraint equation to be differentiated: aimc.airGapS.i_ms[1] = aimc.lssigma.i_[1] + aimc.idq_rs[1] Differentiated equation: der(aimc.airGapS.i_ms[1]) = der(aimc.lssigma.i_[1]) + der(aimc.idq_rs[1]) Update Incidence Matrix: 219 230 228 227 224 222 221 225 223 226 220 229 218
Differential dependencies are beeing plotted.
########################### STATE SELECTION ########################### State Order: (9) ============= loadTorque.phi ---d/dt---> loadInertia.w loadInertia.w ---d/dt---> loadInertia.a aimc.airGapS.psi_mr[2] ---d/dt---> aimc.airGapS.spacePhasor_r.v_[2] aimc.airGapS.psi_mr[1] ---d/dt---> aimc.airGapS.spacePhasor_r.v_[1] aimc.airGapS.psi_ms[2] ---d/dt---> aimc.airGapS.spacePhasor_s.v_[2] aimc.airGapS.psi_ms[1] ---d/dt---> aimc.airGapS.spacePhasor_s.v_[1] aimc.strayLoad.phi ---d/dt---> aimc.strayLoad.w aimc.friction.phi ---d/dt---> aimc.friction.w aimc.phiMechanical ---d/dt---> aimc.wMechanical
Static state selection with matching (only considering linear occuring states).
Plot order:
- States candidates
- Constraint equations
- Adjacency Matrix (+ transposed)
- Matching
########## Try static state selection ########## Try to select dummy vars with natural matching (newer) Select 16 dummy states from 27 andidates. Highest order derivatives (state candidates): (27) ======================================== 1: aimc.airGapS.gamma:STATE(1)(unit = "rad" ) "Rotor displacement angle" type: Real 2: aimc.airGapS.RotationMatrix[2,1]:STATE(1)() "Matrix of rotation from rotor to stator" type: Real [2,2] 3: aimc.airGapS.RotationMatrix[2,2]:STATE(1)() "Matrix of rotation from rotor to stator" type: Real [2,2] 4: aimc.idq_rs[1]:STATE(1)(unit = "A" ) "Rotor space phasor current / stator fixed frame" type: Real [2] 5: aimc.idq_rs[2]:STATE(1)(unit = "A" ) "Rotor space phasor current / stator fixed frame" type: Real [2] 6: aimc.lssigma.i_[1]:STATE(1)(unit = "A" ) type: Real [2] 7: aimc.lssigma.i_[2]:STATE(1)(unit = "A" ) type: Real [2] 8: aimc.airGapS.i_ms[1]:STATE(1)(unit = "A" ) "Magnetizing current space phasor with respect to the stator fixed frame" type: Real [2] 9: aimc.airGapS.i_ms[2]:STATE(1)(unit = "A" ) "Magnetizing current space phasor with respect to the stator fixed frame" type: Real [2] 10: inductor.inductor[1].i:STATE(1)(start = 0.0 unit = "A" ) "Current flowing from pin p to pin n" type: Real [3] 11: inductor.inductor[2].i:STATE(1)(start = 0.0 unit = "A" ) "Current flowing from pin p to pin n" type: Real [3] 12: inductor.inductor[3].i:STATE(1)(start = 0.0 unit = "A" ) "Current flowing from pin p to pin n" type: Real [3] 13: loadInertia.w:STATE(1,loadInertia.a)(unit = "rad/s" ) "Absolute angular velocity of component (= der(phi))" type: Real 14: aimc.friction.phi:STATE(1,aimc.friction.w)(unit = "rad" ) "Angle between shaft and support" type: Real 15: aimc.strayLoad.phi:STATE(1,aimc.strayLoad.w)(unit = "rad" ) "Angle between shaft and support" type: Real 16: aimc.airGapS.psi_ms[1]:STATE(1,aimc.airGapS.spacePhasor_s.v_[1])(unit = "Wb" ) "Magnetizing flux phasor with respect to the stator fixed frame" type: Real [2] 17: aimc.airGapS.psi_ms[2]:STATE(1,aimc.airGapS.spacePhasor_s.v_[2])(unit = "Wb" ) "Magnetizing flux phasor with respect to the stator fixed frame" type: Real [2] 18: aimc.airGapS.psi_mr[1]:STATE(1,aimc.airGapS.spacePhasor_r.v_[1])(unit = "Wb" ) "Magnetizing flux phasor with respect to the rotor fixed frame" type: Real [2] 19: aimc.airGapS.psi_mr[2]:STATE(1,aimc.airGapS.spacePhasor_r.v_[2])(unit = "Wb" ) "Magnetizing flux phasor with respect to the rotor fixed frame" type: Real [2] 20: capacitor.v:STATE(1)(start = VDC unit = "V" fixed = true ) "Voltage drop of the two pins (= p.v - n.v)" type: Real 21: vfController.x:STATE(1)(start = 0.0 unit = "rad" fixed = true ) "Integrator state" type: Real 22: aimc.idq_sr[1]:STATE(1)(unit = "A" stateSelect=StateSelect.prefer ) "Stator space phasor current / rotor fixed frame" type: Real [2] 23: aimc.idq_sr[2]:STATE(1)(unit = "A" stateSelect=StateSelect.prefer ) "Stator space phasor current / rotor fixed frame" type: Real [2] 24: aimc.idq_rr[1]:STATE(1)(unit = "A" stateSelect=StateSelect.prefer ) "Rotor space phasor current / rotor fixed frame" type: Real [2] 25: aimc.idq_rr[2]:STATE(1)(unit = "A" stateSelect=StateSelect.prefer ) "Rotor space phasor current / rotor fixed frame" type: Real [2] 26: aimc.phiMechanical:STATE(1,aimc.wMechanical)(start = 0.0 unit = "rad" fixed = true ) "Mechanical angle of rotor against stator" type: Real 27: aimc.i_0_s:STATE(1)(start = 0.0 unit = "A" stateSelect=StateSelect.prefer ) "Stator zero-sequence current" type: Real Constraint equations: (16) ======================================== 1/1 (1): aimc.idq_rs[2] = aimc.airGapS.RotationMatrix[2,1] * aimc.idq_rr[1] + aimc.airGapS.RotationMatrix[2,2] * aimc.idq_rr[2] [dynamic |0|0|0|0|] 2/2 (1): aimc.idq_rs[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.idq_rr[1] - aimc.airGapS.RotationMatrix[2,1] * aimc.idq_rr[2] [dynamic |0|0|0|0|] 3/3 (1): aimc.lssigma.i_[2] = aimc.airGapS.RotationMatrix[2,1] * aimc.idq_sr[1] + aimc.airGapS.RotationMatrix[2,2] * aimc.idq_sr[2] [dynamic |0|0|0|0|] 4/4 (1): aimc.lssigma.i_[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.idq_sr[1] - aimc.airGapS.RotationMatrix[2,1] * aimc.idq_sr[2] [dynamic |0|0|0|0|] 5/5 (1): -aimc.airGapS.RotationMatrix[2,1] = -sin(aimc.airGapS.gamma) [dynamic |0|0|0|0|] 6/6 (1): aimc.airGapS.RotationMatrix[2,2] = cos(aimc.airGapS.gamma) [dynamic |0|0|0|0|] 7/7 (1): aimc.airGapS.gamma = /*Real*/(aimc.airGapS.p) * (loadTorque.phi - aimc.fixed.phi0) [dynamic |0|0|0|0|] 8/8 (1): aimc.airGapS.psi_mr[2] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.psi_ms[2] - aimc.airGapS.RotationMatrix[2,1] * aimc.airGapS.psi_ms[1] [dynamic |0|0|0|0|] 9/9 (1): aimc.airGapS.psi_mr[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.psi_ms[1] + aimc.airGapS.RotationMatrix[2,1] * aimc.airGapS.psi_ms[2] [dynamic |0|0|0|0|] 10/10 (1): aimc.airGapS.psi_ms[2] = aimc.airGapS.L[2,1] * aimc.airGapS.i_ms[1] + aimc.airGapS.L[2,2] * aimc.airGapS.i_ms[2] [dynamic |0|0|0|0|] 11/11 (1): aimc.airGapS.psi_ms[1] = aimc.airGapS.L[1,1] * aimc.airGapS.i_ms[1] + aimc.airGapS.L[1,2] * aimc.airGapS.i_ms[2] [dynamic |0|0|0|0|] 12/12 (1): aimc.airGapS.i_ms[2] = aimc.lssigma.i_[2] + aimc.idq_rs[2] [dynamic |0|0|0|0|] 13/13 (1): aimc.airGapS.i_ms[1] = aimc.lssigma.i_[1] + aimc.idq_rs[1] [dynamic |0|0|0|0|] 14/14 (1): aimc.strayLoad.phi = loadTorque.phi - aimc.fixed.phi0 [dynamic |0|0|0|0|] 15/15 (1): aimc.friction.phi = loadTorque.phi - aimc.fixed.phi0 [dynamic |0|0|0|0|] 16/16 (1): aimc.phiMechanical = loadTorque.phi - aimc.fixed.phi0 [binding |0|0|0|0|] Adjacency Matrix Enhanced (row == equation) ==================================== number of rows: 16 1:(-5,solved) (-2,variable(true)) (-24,variable(true)) (-3,variable(true)) (-25,variable(true)) 2:(-4,solved) (-3,variable(true)) (-24,variable(true)) (-2,variable(true)) (-25,variable(true)) 3:(-7,solved) (-2,variable(true)) (-22,variable(true)) (-3,variable(true)) (-23,variable(true)) 4:(-6,solved) (-3,variable(true)) (-22,variable(true)) (-2,variable(true)) (-23,variable(true)) 5:(-2,solved) (-1,nonlinear) 6:(-3,solved) (-1,nonlinear) 7:(-1,solved) 8:(-19,solved) (-3,variable(true)) (-17,variable(true)) (-2,variable(true)) (-16,variable(true)) 9:(-18,solved) (-3,variable(true)) (-16,variable(true)) (-2,variable(true)) (-17,variable(true)) 10:(-17,solved) (-8,param(false)) (-9,param(true)) 11:(-16,solved) (-8,param(true)) (-9,param(false)) 12:(-9,solved) (-7,constone) (-5,constone) 13:(-8,solved) (-6,constone) (-4,constone) 14:(-15,solved) 15:(-14,solved) 16:(-26,solved) Transpose Adjacency Matrix Enhanced (row == var) ===================================== number of rows: 27 1:(-7,solved) (-6,nonlinear) (-5,nonlinear) 2:(-9,variable(true)) (-8,variable(true)) (-5,solved) (-4,variable(true)) (-3,variable(true)) (-2,variable(true)) (-1,variable(true)) 3:(-9,variable(true)) (-8,variable(true)) (-6,solved) (-4,variable(true)) (-3,variable(true)) (-2,variable(true)) (-1,variable(true)) 4:(-13,constone) (-2,solved) 5:(-12,constone) (-1,solved) 6:(-13,constone) (-4,solved) 7:(-12,constone) (-3,solved) 8:(-13,solved) (-11,param(true)) (-10,param(false)) 9:(-12,solved) (-11,param(false)) (-10,param(true)) 10: 11: 12: 13: 14:(-15,solved) 15:(-14,solved) 16:(-11,solved) (-9,variable(true)) (-8,variable(true)) 17:(-10,solved) (-9,variable(true)) (-8,variable(true)) 18:(-9,solved) 19:(-8,solved) 20: 21: 22:(-4,variable(true)) (-3,variable(true)) 23:(-4,variable(true)) (-3,variable(true)) 24:(-2,variable(true)) (-1,variable(true)) 25:(-2,variable(true)) (-1,variable(true)) 26:(-16,solved) 27: Matching ======================================== 27 variables and equations var 1 is solved in eqn 7 var 2 is solved in eqn 5 var 3 is solved in eqn 6 var 4 is solved in eqn 2 var 5 is solved in eqn 1 var 6 is solved in eqn 4 var 7 is solved in eqn 3 var 8 is solved in eqn 13 var 9 is solved in eqn 12 var 10 is solved in eqn -1 var 11 is solved in eqn -1 var 12 is solved in eqn -1 var 13 is solved in eqn -1 var 14 is solved in eqn 15 var 15 is solved in eqn 14 var 16 is solved in eqn 11 var 17 is solved in eqn 10 var 18 is solved in eqn 9 var 19 is solved in eqn 8 var 20 is solved in eqn -1 var 21 is solved in eqn -1 var 22 is solved in eqn -1 var 23 is solved in eqn -1 var 24 is solved in eqn -1 var 25 is solved in eqn -1 var 26 is solved in eqn 16 var 27 is solved in eqn -1 Matching ======================================== 16 variables and equations var 1 is solved in eqn 5 var 2 is solved in eqn 4 var 3 is solved in eqn 7 var 4 is solved in eqn 6 var 5 is solved in eqn 2 var 6 is solved in eqn 3 var 7 is solved in eqn 1 var 8 is solved in eqn 19 var 9 is solved in eqn 18 var 10 is solved in eqn 17 var 11 is solved in eqn 16 var 12 is solved in eqn 9 var 13 is solved in eqn 8 var 14 is solved in eqn 15 var 15 is solved in eqn 14 var 16 is solved in eqn 26
States that get selected as dummy states.
Selected dummy states: (16) ======================================== 1: aimc.phiMechanical:STATE(1,aimc.wMechanical)(start = 0.0 unit = "rad" fixed = true ) "Mechanical angle of rotor against stator" type: Real 2: aimc.airGapS.psi_mr[2]:STATE(1,aimc.airGapS.spacePhasor_r.v_[2])(unit = "Wb" ) "Magnetizing flux phasor with respect to the rotor fixed frame" type: Real [2] 3: aimc.airGapS.psi_mr[1]:STATE(1,aimc.airGapS.spacePhasor_r.v_[1])(unit = "Wb" ) "Magnetizing flux phasor with respect to the rotor fixed frame" type: Real [2] 4: aimc.airGapS.psi_ms[2]:STATE(1,aimc.airGapS.spacePhasor_s.v_[2])(unit = "Wb" ) "Magnetizing flux phasor with respect to the stator fixed frame" type: Real [2] 5: aimc.airGapS.psi_ms[1]:STATE(1,aimc.airGapS.spacePhasor_s.v_[1])(unit = "Wb" ) "Magnetizing flux phasor with respect to the stator fixed frame" type: Real [2] 6: aimc.strayLoad.phi:STATE(1,aimc.strayLoad.w)(unit = "rad" ) "Angle between shaft and support" type: Real 7: aimc.friction.phi:STATE(1,aimc.friction.w)(unit = "rad" ) "Angle between shaft and support" type: Real 8: aimc.airGapS.i_ms[2]:STATE(1)(unit = "A" ) "Magnetizing current space phasor with respect to the stator fixed frame" type: Real [2] 9: aimc.airGapS.i_ms[1]:STATE(1)(unit = "A" ) "Magnetizing current space phasor with respect to the stator fixed frame" type: Real [2] 10: aimc.lssigma.i_[2]:STATE(1)(unit = "A" ) type: Real [2] 11: aimc.lssigma.i_[1]:STATE(1)(unit = "A" ) type: Real [2] 12: aimc.idq_rs[2]:STATE(1)(unit = "A" ) "Rotor space phasor current / stator fixed frame" type: Real [2] 13: aimc.idq_rs[1]:STATE(1)(unit = "A" ) "Rotor space phasor current / stator fixed frame" type: Real [2] 14: aimc.airGapS.RotationMatrix[2,2]:STATE(1)() "Matrix of rotation from rotor to stator" type: Real [2,2] 15: aimc.airGapS.RotationMatrix[2,1]:STATE(1)() "Matrix of rotation from rotor to stator" type: Real [2,2] 16: aimc.airGapS.gamma:STATE(1)(unit = "rad" ) "Rotor displacement angle" type: Real
Static selection succeeds.
Perfect Matching, no dynamic index reduction needed! There are no unassigned equations.
@Francesco I don't think, that this is what you would expect happening right? The mentioned equation
inductor.inductor[1].i+inductor.inductor[2].i+inductor.inductor[3].i- inductor1.i = 0.0;
does not appear at all and the containing variables can therefore never be chosen as dummys since they actually don't appear in any other constraint equations. My guess is that the matching does not identify the MSSS correct or passes incomplete information.
I will provide the outputs for the smaller models shortly.
follow-ups: 12 13 comment:11 by , 7 years ago
As mentioned in comment:9, I'm still unsure of what exactly the state constraint equation should be in the MSL example, but there is no question that there is some constraint equation involving the inductor currents, since there is at least one star connection involving them in the system.
So, it is quite strange that I don't see anything related to them in the MSSS. Maybe the output for the smaller models will shed some more light, since at least in the first example it seems that the correct index reduction is carried out, so we should see something.
BTW, I'm not too familiar with the concept of MSSS and their relationship with index reduction, do you have any reference to point to me so I can learn a bit more?
comment:12 by , 7 years ago
Replying to casella:
BTW, I'm not too familiar with the concept of MSSS and their relationship with index reduction, do you have any reference to point to me so I can learn a bit more?
Index reduction basically is a backup mechanism for matching, to solve structural singularities. When trying to match the system so called "minimal structural singular subsets", which are a set of n equations containing at most n-1 unknowns, get collected. These are the constraint equations and corresponding state candidates. Since these equations overdetermine the candidates there must be an underdetermined part in the system.
All those get derived and dummys are chosen by analyzing the jacobian of all constraint equations derived by all candidates.
If you are familiar with pantelides algorithm this might help:
The MSSS contains all equations and variables that are marked at the moment the algorithm fails to match a certain equation while traversing the bipartite graph.
EDIT:
Best to understand reading Pantelides original paper from
https://epubs.siam.org/doi/10.1137/0909014
MSS are first mentioned at side 10
comment:13 by , 7 years ago
Replying to casella:
Maybe the output for the smaller models will shed some more light, since at least in the first example it seems that the correct index reduction is carried out, so we should see something.
For the first model TestIndexReduction.mo it is straight forward:
unmatched equations: 32 Index Reduction neccessary! MSS subsets: 32 ##############--MSSS--############## Indices of constraint equations: 32 ------------------32------------------ Constraint equation to be differentiated: inductor.inductor[1].i + inductor.inductor[2].i + inductor.inductor[3].i - inductor1.i = 0.0 Differentiated equation: der(inductor.inductor[1].i) + der(inductor.inductor[2].i) + der(inductor.inductor[3].i) - der(inductor1.i) = 0.0 Update Incidence Matrix: 32 ########################### STATE SELECTION ########################### ########## Try static state selection ########## Try to select dummy vars with natural matching (newer) Select 1 dummy states from 4 candidates. Highest order derivatives (state candidates): (4) ======================================== 1: inductor.inductor[1].i:STATE(1)(start = 0.0 unit = "A" ) "Current flowing from pin p to pin n" type: Real [3] 2: inductor.inductor[2].i:STATE(1)(start = 0.0 unit = "A" ) "Current flowing from pin p to pin n" type: Real [3] 3: inductor.inductor[3].i:STATE(1)(start = 0.0 unit = "A" ) "Current flowing from pin p to pin n" type: Real [3] 4: inductor1.i:STATE(1)(start = 0.0 unit = "A" ) "Current flowing from pin p to pin n" type: Real Constraint equations: (1) ======================================== 1/1 (1): inductor.inductor[1].i + inductor.inductor[2].i + inductor.inductor[3].i - inductor1.i = 0.0 [dynamic |0|0|0|0|] Adjacency Matrix Enhanced (row == equation) ==================================== number of rows: 1 1:(-1,constone) (-2,constone) (-3,constone) (-4,constone) Transpose Adjacency Matrix Enhanced (row == var) ===================================== number of rows: 4 1:(-1,constone) 2:(-1,constone) 3:(-1,constone) 4:(-1,constone) Matching ======================================== 4 variables and equations var 1 is solved in eqn 1 var 2 is solved in eqn -1 var 3 is solved in eqn -1 var 4 is solved in eqn -1 Matching ======================================== 1 variables and equations var 1 is solved in eqn 1 Selected dummy states: (1) ======================================== 1: inductor.inductor[1].i:STATE(1)(start = 0.0 unit = "A" ) "Current flowing from pin p to pin n" type: Real [3] Perfect Matching, no dynamic index reduction needed! There are no unassigned equations.
It seems like this is exactly what dymola does. For the second example it fails before even getting to index reduction, therefore no output is generated. It seems like it fails while matching. I will try to find out what the differences are.
follow-up: 15 comment:14 by , 7 years ago
Ok. So, for the following index-2 model
model M parameter Real q0; Real p1, p2, q; equation der(p1) = q0 - q; der(p2) = q; p1 = p2; end M;
assuming no alias elimination is performed, the MSSS wil be p1 = p2, and of course the rest of the system is underdetermined because q has no equation to be solved in.
Is that correct?
comment:15 by , 7 years ago
Replying to casella:
Ok. So, for the following index-2 model
model M parameter Real q0; Real p1, p2, q; equation der(p1) = q0 - q; der(p2) = q; p1 = p2; end M;assuming no alias elimination is performed, the MSSS wil be
p1 = p2, and of course the rest of the system is underdetermined because q has no equation to be solved in.
Is that correct?
Yes exactly.
follow-ups: 19 22 24 comment:17 by , 7 years ago
I have difficulties testing TestIndexReduction (and TestIndexReduction2)
due to problems with my actually installed nightly build version of OpenModelica
which claims:
[/var/lib/jenkins1/ws/LINUX_BUILDS/tmp.build/openmodelica-1.14.0~dev-26555-g4698d26/
OMCompiler/Compiler/NFFrontEnd/NFCeval.mo: 888:9-888:67]:
Internal error NFCeval.evalBinaryMul failed to evaluate
‘6.283185307179586 * {50.0, 50.0, 50.0}‘
Does this need a different ticket?
However, to me the key models in the index reduction problem of Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive seem to be the rectifier and the inverter -- and their particular connection.
In principal both the rectifier and the inverter behave the same, except for the
different semiconductors used and the different switching patterns.
The rectifer has one three-phase AC plug ac and two analog singe-phase (DC) pins, i.e.
dc_p and dc_n. So Kirchhoffs law states
that the sum of the three AC currents plus the two DC currents must be zero. The same applies to the
inverter model. As there is no grounding in the DC intermediate circuit, the following
equation applies to the two DC currents of the rectifier and the inverter:
rectifier.dc_p.i + rectifier.dc_n.i = 0; inverter.dc_p.i + inverter.dc_n.i = 0;
All five currents of the rectifier have to sum up to zero due to Kirchhoffs law. The sum of the two DC currents is equal to zero, too. Then the sum of the three AC currents, of the rectifier and inverter has to be zero as well:
rectifier.ac.pin[1].i + rectifier.ac.pin[2].i + rectifier.ac.pin[3].i = 0; inverter.ac.pin[1].i + inverter.ac.pin[2].i + inverter.ac.pin[3].i = 0;
As the machine aimc is delta connected, the sum of the three voltages of the machine is equal to zero:
aimc.vs[1] + aimc.vs[2] + aimc.vs[3] = 0;
A similar condition does not apply the three machine phase currents aimc.is
as a circular (zero) current component may occur, which is equal in all three phases.
comment:18 by , 7 years ago
| Cc: | added |
|---|
comment:19 by , 7 years ago
Replying to Christian Kral <dr.christian.kral@…>:
I have difficulties testing
TestIndexReduction(andTestIndexReduction2)
due to problems with my actually installed nightly build version of OpenModelica
which claims:
[/var/lib/jenkins1/ws/LINUX_BUILDS/tmp.build/openmodelica-1.14.0~dev-26555-g4698d26/ OMCompiler/Compiler/NFFrontEnd/NFCeval.mo: 888:9-888:67]: Internal error NFCeval.evalBinaryMul failed to evaluate ‘6.283185307179586 * {50.0, 50.0, 50.0}‘
I'm using v1.14.0-dev-26534-g3ae6d2dc06 (64-bit) (17/06/2019) and it works fine. Maybe you need to install a more recent nightly, there may be some problems with the NF that have been solved recently. Or to disable the new front-end, the examples work (or don't work) also with the old one.
follow-up: 23 comment:20 by , 7 years ago
OK. I disabled the new experimental instantiation phase and now the model translates. And fails with a singular matrix.
I made the following modification to Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive: I added an analog resistor with R = 10E3 Ohm to the circuit and connected one pin with the capacitor. I then added a second ground and connected it to the other pin of the newly added resistor. This then allows that the two DC currents of the positive and negative pin do not have to be the same (with different sign) any more.
With this additional resistor and ground the model compiles and starts simulating. It then fails with NO singular matrix error. Instead I get:
The initialization finished successfully without homotopy method. Simulation terminated due to too many, i.e. 20, event iterations. This could either indicate an inconsistent system or an undersized limit of event iterations. The limit of event iterations can be specified using the runtime flag '–mei=<value>'. Simulation process failed. Exited with code 255.
comment:22 by , 7 years ago
Replying to Christian Kral <dr.christian.kral@…>:
As the machine
aimcis delta connected, the sum of the three voltages of the machine is equal to zero:
aimc.vs[1] + aimc.vs[2] + aimc.vs[3] = 0;
Aha, I missed that.
I prepared two updated test models TestIndexReduction3 and TestIndexReduction4 where I terminated the circuits with a delta-connected resistive load, which more accurately reflects the structure of the original MSL model.
In the case without rectifier and inverter (TestIndexReduction3), OMC correctly identifies the constraint and performs the right index reduction. In the other case TestIndexReduction4 it fails to do so and ends up with an index-2 DAE, that causes the runtime solver to fail.
@Karim, I would suggest that you use these two examples for your analysis, as they are closer to the original MSra model while avoiding one extra state variable.
by , 7 years ago
| Attachment: | TestIndexReduction3.mo added |
|---|
by , 7 years ago
| Attachment: | TestIndexReduction4.mo added |
|---|
comment:23 by , 7 years ago
Replying to dr.christian.kral@…:
I made the following modification to
Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive: I added an analog resistor with R = 10E3 Ohm to the circuit and connected one pin with the capacitor. I then added a second ground and connected it to the other pin of the newly added resistor. This then allows that the two DC currents of the positive and negative pin do not have to be the same (with different sign) any more.
This is an interesting case, but we must make sure OMC can solve the original one, if we want to achieve the goal of 100% MSL coverage.
With this additional resistor and ground the model compiles and starts simulating. It then fails with NO singular matrix error. Instead I get:
The initialization finished successfully without homotopy method. Simulation terminated due to too many, i.e. 20, event iterations. This could either indicate an inconsistent system or an undersized limit of event iterations. The limit of event iterations can be specified using the runtime flag '–mei=<value>'. Simulation process failed. Exited with code 255.
I think before investigating this issue we should sort out the previous one. My educated guess is that once that is solved, this last model of yours may also work.
follow-up: 25 comment:24 by , 7 years ago
Replying to Christian Kral <dr.christian.kral@…>: Just to make this clear again: As I understand your were -- among other things -- originally looking for the missing equation:
inductor.inductor[1].i+inductor.inductor[2].i+inductor.inductor[3].i = 0.0;
This equation is equivalent to:
rectifier.ac.pin[1].i + rectifier.ac.pin[2].i + rectifier.ac.pin[3].i = 0.0;
So I suppose this is your missing equation.
comment:25 by , 7 years ago
Replying to dr.christian.kral@…:
Just to make this clear again: As I understand your were -- among other things -- originally looking for the missing equation:
inductor.inductor[1].i+inductor.inductor[2].i+inductor.inductor[3].i = 0.0;This equation is equivalent to:
rectifier.ac.pin[1].i + rectifier.ac.pin[2].i + rectifier.ac.pin[3].i = 0.0;So I suppose this is your missing equation.
Sure. The problem is, this equation does not show up in the flattened model either. As far as I understand, the constraint equation is eventually due to the delta-connection at the end of the circuit, and then the backend must somehow propagate this through the various Kirchhoff equations all the way up to the three inductor currents, which are the ones that have the derivative operator applied to.
I'll leave it to Karim to figure out why this doesn't happen with the current OMC backend :)
comment:26 by , 7 years ago
@Karim, I managed to come up with a smaller model that reproduces the missing index reduction, see TestIndexReduction5. I am more and more convinced that the problem is that the backend cannot follow the current constraints in the diode equations of the rectifier.
The system has only three potential states, the three inductor currents, and an overall constraint that the sum of the three currents is zero, so that one of those states should be taken as a dummy.
I hope this model is small enough that we can debug it effectively.
by , 7 years ago
| Attachment: | TestIndexReduction5.mo added |
|---|
follow-up: 28 comment:27 by , 7 years ago
Maybe related to https://trac.openmodelica.org/OpenModelica/ticket/4535.
I would try resolveLoops.
comment:28 by , 7 years ago
Replying to vitalij:
Maybe related to https://trac.openmodelica.org/OpenModelica/ticket/4535.
I would tryresolveLoops.
Unfortunately it did not resolve the problem, but i think you are right and it is related to that ticket. I found following loop in the new smaller system of TestIndexReduction5.mo:
Tearing Variables: ------------------------------------- rectifier.dc_n.v(44), rectifier.diode_n.idealDiode[1].s(12), rectifier.diode_p.idealDiode[3].s(22), rectifier.diode_p.idealDiode[1].s(30), rectifier.diode_n.idealDiode[2].s(8), rectifier.diode_p.idealDiode[2].s(26), rectifier.diode_n.idealDiode[3].s(4) Residual Equations: ------------------------------------- 4: vSource.V = rectifier.dc_p.v - rectifier.dc_n.v; 3: rectifier.diode_p.i[3] + (-rectifier.diode_n.i[3]) - inductor.inductor[3].i = 0.0; 2: rectifier.diode_p.i[2] + (-rectifier.diode_n.i[2]) - inductor.inductor[2].i = 0.0; 6: (-rectifier.diode_n.i[2]) - rectifier.diode_n.i[1] - rectifier.iDC - rectifier.diode_n.i[3] = 0.0; 45: rectifier.vDC = rectifier.dc_p.v - rectifier.dc_n.v; 21: 0.0 = rectifier.vDC + rectifier.dc_n.v + (-rectifier.dc_p.v) - vSource.V - rectifier.diode_p.idealDiode[1].v - rectifier.diode_n.idealDiode[1].v; 1: rectifier.diode_p.i[1] + (-rectifier.diode_n.i[1]) - inductor.inductor[1].i = 0.0; Inner Variables: ------------------------------------- rectifier.dc_p.v(45),rectifier.iDC(42),rectifier.vDC(43),rectifier.diode_n.idealDiode[3].v(7),rectifier.diode_n.i[3](16),rectifier.diode_n.idealDiode[3].off(5),rectifier.diode_p.idealDiode[2].v(29),rectifier.diode_p.i[2](35),rectifier.diode_p.idealDiode[2].off(27),rectifier.diode_n.i[2](17),rectifier.diode_n.idealDiode[2].v(11),rectifier.diode_n.idealDiode[2].off(9),rectifier.diode_p.idealDiode[1].v(33),rectifier.diode_p.i[1](36),rectifier.diode_p.idealDiode[1].off(31),rectifier.diode_p.i[3](34),rectifier.diode_p.idealDiode[3].v(25),rectifier.diode_p.idealDiode[3].off(23),rectifier.diode_n.idealDiode[1].v(15),rectifier.diode_n.i[1](18),rectifier.diode_n.idealDiode[1].off(13), InnerEquations: ------------------------------------- 11: 0.0 = rectifier.vDC + rectifier.diode_p.idealDiode[2].v + rectifier.diode_n.idealDiode[2].v + rectifier.dc_p.v + rectifier.diode_p.idealDiode[3].v + rectifier.diode_n.idealDiode[3].v + (-rectifier.dc_n.v) - vSource.V - rectifier.diode_p.idealDiode[1].v - rectifier.diode_n.idealDiode[1].v; 7: rectifier.diode_p.i[1] + rectifier.diode_p.i[2] + rectifier.diode_p.i[3] + rectifier.iDC = 0.0; 16: 0.0 = rectifier.vDC + rectifier.diode_p.idealDiode[2].v + rectifier.diode_n.idealDiode[2].v + (-vSource.V) - rectifier.diode_p.idealDiode[1].v - rectifier.diode_n.idealDiode[1].v; 14: rectifier.diode_n.idealDiode[3].v = rectifier.diode_n.idealDiode[3].s * (if rectifier.diode_n.idealDiode[3].off then 1.0 else rectifier.diode_n.idealDiode[3].Ron) + rectifier.diode_n.idealDiode[3].Vknee; 13: rectifier.diode_n.i[3] = rectifier.diode_n.idealDiode[3].s * (if rectifier.diode_n.idealDiode[3].off then rectifier.diode_n.idealDiode[3].Goff else 1.0) + rectifier.diode_n.idealDiode[3].Goff * rectifier.diode_n.idealDiode[3].Vknee; 15: rectifier.diode_n.idealDiode[3].off = rectifier.diode_n.idealDiode[3].s < 0.0; 37: rectifier.diode_p.idealDiode[2].v = rectifier.diode_p.idealDiode[2].s * (if rectifier.diode_p.idealDiode[2].off then 1.0 else rectifier.diode_p.idealDiode[2].Ron) + rectifier.diode_p.idealDiode[2].Vknee; 36: rectifier.diode_p.i[2] = rectifier.diode_p.idealDiode[2].s * (if rectifier.diode_p.idealDiode[2].off then rectifier.diode_p.idealDiode[2].Goff else 1.0) + rectifier.diode_p.idealDiode[2].Goff * rectifier.diode_p.idealDiode[2].Vknee; 38: rectifier.diode_p.idealDiode[2].off = rectifier.diode_p.idealDiode[2].s < 0.0; 18: rectifier.diode_n.i[2] = rectifier.diode_n.idealDiode[2].s * (if rectifier.diode_n.idealDiode[2].off then rectifier.diode_n.idealDiode[2].Goff else 1.0) + rectifier.diode_n.idealDiode[2].Goff * rectifier.diode_n.idealDiode[2].Vknee; 19: rectifier.diode_n.idealDiode[2].v = rectifier.diode_n.idealDiode[2].s * (if rectifier.diode_n.idealDiode[2].off then 1.0 else rectifier.diode_n.idealDiode[2].Ron) + rectifier.diode_n.idealDiode[2].Vknee; 20: rectifier.diode_n.idealDiode[2].off = rectifier.diode_n.idealDiode[2].s < 0.0; 42: rectifier.diode_p.idealDiode[1].v = rectifier.diode_p.idealDiode[1].s * (if rectifier.diode_p.idealDiode[1].off then 1.0 else rectifier.diode_p.idealDiode[1].Ron) + rectifier.diode_p.idealDiode[1].Vknee; 41: rectifier.diode_p.i[1] = rectifier.diode_p.idealDiode[1].s * (if rectifier.diode_p.idealDiode[1].off then rectifier.diode_p.idealDiode[1].Goff else 1.0) + rectifier.diode_p.idealDiode[1].Goff * rectifier.diode_p.idealDiode[1].Vknee; 43: rectifier.diode_p.idealDiode[1].off = rectifier.diode_p.idealDiode[1].s < 0.0; 31: rectifier.diode_p.i[3] = rectifier.diode_p.idealDiode[3].s * (if rectifier.diode_p.idealDiode[3].off then rectifier.diode_p.idealDiode[3].Goff else 1.0) + rectifier.diode_p.idealDiode[3].Goff * rectifier.diode_p.idealDiode[3].Vknee; 32: rectifier.diode_p.idealDiode[3].v = rectifier.diode_p.idealDiode[3].s * (if rectifier.diode_p.idealDiode[3].off then 1.0 else rectifier.diode_p.idealDiode[3].Ron) + rectifier.diode_p.idealDiode[3].Vknee; 33: rectifier.diode_p.idealDiode[3].off = rectifier.diode_p.idealDiode[3].s < 0.0; 24: rectifier.diode_n.idealDiode[1].v = rectifier.diode_n.idealDiode[1].s * (if rectifier.diode_n.idealDiode[1].off then 1.0 else rectifier.diode_n.idealDiode[1].Ron) + rectifier.diode_n.idealDiode[1].Vknee; 23: rectifier.diode_n.i[1] = rectifier.diode_n.idealDiode[1].s * (if rectifier.diode_n.idealDiode[1].off then rectifier.diode_n.idealDiode[1].Goff else 1.0) + rectifier.diode_n.idealDiode[1].Goff * rectifier.diode_n.idealDiode[1].Vknee; 25: rectifier.diode_n.idealDiode[1].off = rectifier.diode_n.idealDiode[1].s < 0.0;
Some of the residuals seem to form the constraint we are looking for, i am especially looking at equations 1,2,3 and maybe 6. Those equations seem to be the flow sums that are constructed by connects. The inner equations seem to contain the potential equality (connect) equations and the inner diode equations, which would match Francesco's assumption that the diodes cause the problem.
Maybe there is just missing some form of index reduction containing algebraic loops inbetween?
As mentioned in #4535 we might need an entire new algorithm to solve this kind of problem. Since resolveLoops is mentioned as a possible solution, i will look into it to see what it actually does.
comment:29 by , 7 years ago
I had originally tried -resolveLoops to solve this issue, but to no avail. That's why I put @vwaurich in cc:. However, I didn't look at the backend intermediate debug output.
comment:30 by , 7 years ago
From a physical point of view, the rectifier is built in a way that positive currents run through one branch, while negative currents run through the negative branch. In fact, the diodes have a finite (but very large) resistance when they are blocked, so that a bit of current is also flowing in the other branch. Anyway, the point is that if you take the sum of the current going through those two branches, you get the original inductor current. And this is what happens eventually, when all currents are rerouted through the positive and negative pin of the DC side of the circuit.
follow-up: 32 comment:31 by , 7 years ago
In fact, if you take (1)+(2)+(3)-(6)-(7) in comment:28, most terms cancel out and the only one left are
inductor.inductor[1].i + inductor.inductor[2].i + inductor.inductor[1].i = 0.0
Which is exactly what we are looking for :)
As I understand it, what makes this model different from the ones where omc works is that the current in each of the three conductors is split in two branches. How exactly that is done is irrelevant (the specific diode equations do not enter into the set of constraint equations), what is important is the balance of currents at the connection nodes.
We should investigate why resolveLoops does not figure this out, and extend that algorithm to also handle this case. Then, we should also consider whether to make resolveLoops active by default, as it may be essential in handling some models which are found out there.
Unfortunately we can't think of trying it after index reduction has failed, because the failure is not structural (which could be caught by the backend), but rather numerical, and so only visible at runtime, se we'd need to make sure that
resolveLoopsalways works fine.
follow-up: 34 comment:32 by , 7 years ago
Replying to casella:
In fact, if you take (1)+(2)+(3)-(6)-(7) in comment:28, most terms cancel out and the only one left are
inductor.inductor[1].i + inductor.inductor[2].i + inductor.inductor[1].i = 0.0Which is exactly what we are looking for :)
I build a bipartite graph from the described loop as presented in the paper about reshuffling by @vwaurich and attached it as an image and a graphml version. It seems like the algorithm should be able to handle it, but i have to dig deeper into the algorithm to fully comprehend it. There is one line in the paper i stumpled upon:
The case of having both eqCrossNodes and varCrossNodes in one cycle is practically very uncommon. If it does occur, these cycles are not resolved.
For short reference, crossNodes are nodes with more than two edges. Although it does not look like it applies here (nodes with only one edges are removed beforehand), there may be some correlation we did not take into account.
We should investigate why
resolveLoopsdoes not figure this out, and extend that algorithm to also handle this case. Then, we should also consider whether to makeresolveLoopsactive by default, as it may be essential in handling some models which are found out there.
It seems like this should be activated on default, but i guess it isn't for performance reasons?
by , 7 years ago
| Attachment: | resolveLoopsCycle.bmp added |
|---|
by , 7 years ago
| Attachment: | resolveLoopsCycle.graphml added |
|---|
comment:33 by , 7 years ago
About resolveLoops, see this paper by Volker Waurich et al., EOOLT 2014.
comment:34 by , 7 years ago
Replying to Karim.Abdelhak:
Replying to casella:
We should investigate why
resolveLoopsdoes not figure this out, and extend that algorithm to also handle this case. Then, we should also consider whether to makeresolveLoopsactive by default, as it may be essential in handling some models which are found out there.
It seems like this should be activated on default, but i guess it isn't for performance reasons?
Yes, but also possibly because of experimental status. We should probably try to contact Volker and discuss this with him
comment:35 by , 7 years ago
BTW, I found this additional information in an e-mail exchange with Volker
reshuffling (before casualization) is activated by default but it uses a pretty conservative heuristic to choose the equations which should be resolved.
You can choose between +reshuffle=1/2/3 to change the heuristic. The postOpt-module was an attempt to resolve equations only in algebraic loops, but this turned out to be not very effective.
The module in the backend is actually called resolveLoops. There is the debug-flag resolveLoopsDump that gives some information on the procedure, but this might be solely useful if you look at the corresponding graphs.
I guess we should put this information in the online documentation, if it isn't there already.
comment:36 by , 7 years ago
Summary of today's discussion: the problem could be easily solved by the reshuffling algorithm if the arrays were not expanded.
Once scalarized, there are three loops, and the current resolveLoops algorithm apparently doesn't push hard enough to figure out the loop.
Karim will investigate if it is possible to solve the problem by making the current algorithm push harder.
If not, it's probably not worth wasting time on a new algorithm that works on a scalarized version of the system. Rather, we may (for example) run a vectorized version of removeLoops that just takes into account trivial matchings (whole array of variables with whole array or for-loop of equations) - this would already be good to solve the issue.
In fact, we should come up with a strategy to gradually introduce vectorized handling in the back-end, rather than aiming at a completely vectorized thing that may be ready for use in 5 years (or never).
follow-up: 38 comment:37 by , 7 years ago
I solved the problem presented in TestIndexReduction5.mo, the solver is now able to detect the set of equations (1)+(2)+(3)-(6)-(7) @Francesco mentioned. There were actually two problems:
- Scalarization destroyed useful information (
(1),(2),(3)should be one equation) - Base Loops containing more than 2 equations could not be detected.
Sadly i did not fix the main problem, but i am still trying to push it since it is a useful update. It is most probable that there is another form of loop that cannot be detected right now.
FYI: +reshuffle=1/2/3 changes the criteria for when the loops get resolved. It basically looks at the variables in more than one equation and the variables which only occur once. The difference between those and +reshuffle=1/2/3 decide if it gets resolved or not.
comment:38 by , 7 years ago
Replying to Karim.Abdelhak:
Sadly i did not fix the main problem,
Too bad. I guess you should try to get TestIndexReduction4.mo to work now. Probably the inverter is making the situation more involved.
Maybe the but i am still trying to push it since it is a useful update.
Absolutely!
It is most probable that there is another form of loop that cannot be detected right now.
Yep (see above). The image here
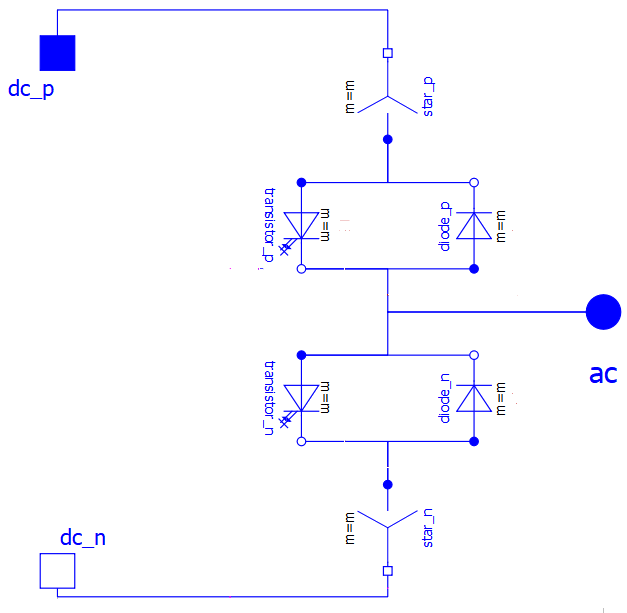
shows the inverter circuit, where I removed all connections except the ones carrying currents. Eventually, as I understand it, the following relationship should be found out by the reshuffling algorithm:
sum(inverter.dc_p.i) + sum(inverter.dc_n.i) + sum(inverter.ac.i) = 0;
I hope you can figure out how to combine all the equations of the inverter involving currents to get this relationship, and then how to get the reshuffling algorithm to find that out.
by , 7 years ago
| Attachment: | Inverter.png added |
|---|
comment:39 by , 7 years ago
| Component: | Code Generation → Backend |
|---|
comment:40 by , 6 years ago
@Karim has a proposal for a good theoretical solution, will discuss it with other people at Bielefeld today
comment:41 by , 6 years ago
I implemented an algorithm that converts analytical to structural singularities and it works as expected for the model Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive. The base replacement that it finds is as follows:
Linear dependent equation: inverter.star_n.plug_p.pin[2].i + inverter.diode_n.i[2] - inverter.transistor_n.i[2] = 0.0 Gets replaced by equation: 0.0 = inverter.iAC[2] + inverter.iAC[1] + inverter.iAC[3] + inductor.inductor[1].i + inductor.inductor[3].i + inductor.inductor[2].i
Which i think is what we expected. The replaced equation is one of the linear dependent ones, it should be okay that it is an arbitrary one from the linear dependent set of equations. Index reduction now recognizes the constraint equations and finds following constraints:
unmatched equations: 172, 176, 216, 218, 222, 224, 227, 228, 230, 278 Index Reduction neccessary! MSS subsets: 278, 285, 284, 283, 206, 208, 212, 214, 213, 207 218, 229, 220, 226, 223, 225, 221, 222, 224, 227, 228, 230, 219 216 176 172 ##############--MSSS--############## Indices of constraint equations: 172 ------------------172------------------ Constraint equation to be differentiated: aimc.phiMechanical = loadTorque.phi - aimc.fixed.phi0 Differentiated equation: aimc.wMechanical = loadInertia.w Update Incidence Matrix: 172 ##############--MSSS--############## Indices of constraint equations: 176 ------------------176------------------ Constraint equation to be differentiated: aimc.friction.phi = loadTorque.phi - aimc.fixed.phi0 Differentiated equation: aimc.friction.w = loadInertia.w Update Incidence Matrix: 176 ##############--MSSS--############## Indices of constraint equations: 216 ------------------216------------------ Constraint equation to be differentiated: aimc.strayLoad.phi = loadTorque.phi - aimc.fixed.phi0 Differentiated equation: aimc.strayLoad.w = loadInertia.w Update Incidence Matrix: 216 ##############--MSSS--############## Indices of constraint equations: 218 229 220 226 223 225 221 222 224 227 228 230 219 ------------------219------------------ Constraint equation to be differentiated: aimc.airGapS.i_ms[2] = aimc.lssigma.i_[2] + aimc.idq_rs[2] Differentiated equation: der(aimc.airGapS.i_ms[2]) = der(aimc.lssigma.i_[2]) + der(aimc.idq_rs[2]) ------------------230------------------ Constraint equation to be differentiated: aimc.idq_rs[2] = aimc.airGapS.RotationMatrix[2,1] * aimc.idq_rr[1] + aimc.airGapS.RotationMatrix[2,2] * aimc.idq_rr[2] Differentiated equation: der(aimc.idq_rs[2]) = aimc.airGapS.RotationMatrix[2,1] * der(aimc.idq_rr[1]) + der(aimc.airGapS.RotationMatrix[2,1]) * aimc.idq_rr[1] + aimc.airGapS.RotationMatrix[2,2] * der(aimc.idq_rr[2]) + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.idq_rr[2] ------------------228------------------ Constraint equation to be differentiated: aimc.lssigma.i_[2] = aimc.airGapS.RotationMatrix[2,1] * aimc.idq_sr[1] + aimc.airGapS.RotationMatrix[2,2] * aimc.idq_sr[2] Differentiated equation: der(aimc.lssigma.i_[2]) = aimc.airGapS.RotationMatrix[2,1] * der(aimc.idq_sr[1]) + der(aimc.airGapS.RotationMatrix[2,1]) * aimc.idq_sr[1] + aimc.airGapS.RotationMatrix[2,2] * der(aimc.idq_sr[2]) + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.idq_sr[2] ------------------227------------------ Constraint equation to be differentiated: aimc.lssigma.i_[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.idq_sr[1] - aimc.airGapS.RotationMatrix[2,1] * aimc.idq_sr[2] Differentiated equation: der(aimc.lssigma.i_[1]) = aimc.airGapS.RotationMatrix[2,2] * der(aimc.idq_sr[1]) + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.idq_sr[1] + (-aimc.airGapS.RotationMatrix[2,1]) * der(aimc.idq_sr[2]) - der(aimc.airGapS.RotationMatrix[2,1]) * aimc.idq_sr[2] ------------------224------------------ Constraint equation to be differentiated: aimc.airGapS.gamma = /*Real*/(aimc.airGapS.p) * (loadTorque.phi - aimc.fixed.phi0) Differentiated equation: der(aimc.airGapS.gamma) = /*Real*/(aimc.airGapS.p) * loadInertia.w ------------------222------------------ Constraint equation to be differentiated: aimc.airGapS.psi_mr[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.psi_ms[1] + aimc.airGapS.RotationMatrix[2,1] * aimc.airGapS.psi_ms[2] Differentiated equation: aimc.airGapS.spacePhasor_r.v_[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.spacePhasor_s.v_[1] + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.airGapS.psi_ms[1] + aimc.airGapS.RotationMatrix[2,1] * aimc.airGapS.spacePhasor_s.v_[2] + der(aimc.airGapS.RotationMatrix[2,1]) * aimc.airGapS.psi_ms[2] ------------------221------------------ Constraint equation to be differentiated: aimc.airGapS.psi_ms[2] = aimc.airGapS.L[2,1] * aimc.airGapS.i_ms[1] + aimc.airGapS.L[2,2] * aimc.airGapS.i_ms[2] Differentiated equation: aimc.airGapS.spacePhasor_s.v_[2] = aimc.airGapS.L[2,1] * der(aimc.airGapS.i_ms[1]) + aimc.airGapS.L[2,2] * der(aimc.airGapS.i_ms[2]) ------------------225------------------ Constraint equation to be differentiated: aimc.airGapS.RotationMatrix[2,2] = cos(aimc.airGapS.gamma) Differentiated equation: der(aimc.airGapS.RotationMatrix[2,2]) = (-sin(aimc.airGapS.gamma)) * der(aimc.airGapS.gamma) ------------------223------------------ Constraint equation to be differentiated: aimc.airGapS.psi_mr[2] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.psi_ms[2] - aimc.airGapS.RotationMatrix[2,1] * aimc.airGapS.psi_ms[1] Differentiated equation: aimc.airGapS.spacePhasor_r.v_[2] = aimc.airGapS.RotationMatrix[2,2] * aimc.airGapS.spacePhasor_s.v_[2] + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.airGapS.psi_ms[2] + (-aimc.airGapS.RotationMatrix[2,1]) * aimc.airGapS.spacePhasor_s.v_[1] - der(aimc.airGapS.RotationMatrix[2,1]) * aimc.airGapS.psi_ms[1] ------------------226------------------ Constraint equation to be differentiated: -aimc.airGapS.RotationMatrix[2,1] = -sin(aimc.airGapS.gamma) Differentiated equation: -der(aimc.airGapS.RotationMatrix[2,1]) = (-cos(aimc.airGapS.gamma)) * der(aimc.airGapS.gamma) ------------------220------------------ Constraint equation to be differentiated: aimc.airGapS.psi_ms[1] = aimc.airGapS.L[1,1] * aimc.airGapS.i_ms[1] + aimc.airGapS.L[1,2] * aimc.airGapS.i_ms[2] Differentiated equation: aimc.airGapS.spacePhasor_s.v_[1] = aimc.airGapS.L[1,1] * der(aimc.airGapS.i_ms[1]) + aimc.airGapS.L[1,2] * der(aimc.airGapS.i_ms[2]) ------------------229------------------ Constraint equation to be differentiated: aimc.idq_rs[1] = aimc.airGapS.RotationMatrix[2,2] * aimc.idq_rr[1] - aimc.airGapS.RotationMatrix[2,1] * aimc.idq_rr[2] Differentiated equation: der(aimc.idq_rs[1]) = aimc.airGapS.RotationMatrix[2,2] * der(aimc.idq_rr[1]) + der(aimc.airGapS.RotationMatrix[2,2]) * aimc.idq_rr[1] + (-aimc.airGapS.RotationMatrix[2,1]) * der(aimc.idq_rr[2]) - der(aimc.airGapS.RotationMatrix[2,1]) * aimc.idq_rr[2] ------------------218------------------ Constraint equation to be differentiated: aimc.airGapS.i_ms[1] = aimc.lssigma.i_[1] + aimc.idq_rs[1] Differentiated equation: der(aimc.airGapS.i_ms[1]) = der(aimc.lssigma.i_[1]) + der(aimc.idq_rs[1]) Update Incidence Matrix: 219 230 228 227 224 222 221 225 223 226 220 229 218 ##############--MSSS--############## Indices of constraint equations: 268 275 274 273 206 208 212 214 213 207 ------------------207------------------ Constraint equation to be differentiated: aimc.spacePhasorS.i[2] * aimc.spacePhasorS.turnsRatio = aimc.is[2] Differentiated equation: der(aimc.spacePhasorS.i[2]) * aimc.spacePhasorS.turnsRatio = der(aimc.is[2]) ------------------213------------------ Constraint equation to be differentiated: aimc.lssigma.i_[1] = aimc.spacePhasorS.TransformationMatrix[1,1] * aimc.spacePhasorS.i[1] + aimc.spacePhasorS.TransformationMatrix[1,2] * aimc.spacePhasorS.i[2] + aimc.spacePhasorS.TransformationMatrix[1,3] * aimc.spacePhasorS.i[3] Differentiated equation: der(aimc.lssigma.i_[1]) = aimc.spacePhasorS.TransformationMatrix[1,1] * der(aimc.spacePhasorS.i[1]) + aimc.spacePhasorS.TransformationMatrix[1,2] * der(aimc.spacePhasorS.i[2]) + aimc.spacePhasorS.TransformationMatrix[1,3] * der(aimc.spacePhasorS.i[3]) ------------------214------------------ Constraint equation to be differentiated: aimc.lssigma.i_[2] = aimc.spacePhasorS.TransformationMatrix[2,1] * aimc.spacePhasorS.i[1] + aimc.spacePhasorS.TransformationMatrix[2,2] * aimc.spacePhasorS.i[2] + aimc.spacePhasorS.TransformationMatrix[2,3] * aimc.spacePhasorS.i[3] Differentiated equation: der(aimc.lssigma.i_[2]) = aimc.spacePhasorS.TransformationMatrix[2,1] * der(aimc.spacePhasorS.i[1]) + aimc.spacePhasorS.TransformationMatrix[2,2] * der(aimc.spacePhasorS.i[2]) + aimc.spacePhasorS.TransformationMatrix[2,3] * der(aimc.spacePhasorS.i[3]) ------------------212------------------ Constraint equation to be differentiated: (-3.0) * aimc.i_0_s = aimc.spacePhasorS.i[1] + aimc.spacePhasorS.i[2] + aimc.spacePhasorS.i[3] Differentiated equation: (-3.0) * der(aimc.i_0_s) = der(aimc.spacePhasorS.i[1]) + der(aimc.spacePhasorS.i[2]) + der(aimc.spacePhasorS.i[3]) ------------------208------------------ Constraint equation to be differentiated: aimc.spacePhasorS.i[3] * aimc.spacePhasorS.turnsRatio = aimc.is[3] Differentiated equation: der(aimc.spacePhasorS.i[3]) * aimc.spacePhasorS.turnsRatio = der(aimc.is[3]) ------------------206------------------ Constraint equation to be differentiated: aimc.spacePhasorS.i[1] * aimc.spacePhasorS.turnsRatio = aimc.is[1] Differentiated equation: der(aimc.spacePhasorS.i[1]) * aimc.spacePhasorS.turnsRatio = der(aimc.is[1]) ------------------273------------------ Constraint equation to be differentiated: inverter.iAC[3] + aimc.is[3] - aimc.is[2] = 0.0 Differentiated equation: der(inverter.iAC[3]) + der(aimc.is[3]) - der(aimc.is[2]) = 0.0 ------------------274------------------ Constraint equation to be differentiated: inverter.iAC[2] + aimc.is[2] - aimc.is[1] = 0.0 Differentiated equation: der(inverter.iAC[2]) + der(aimc.is[2]) - der(aimc.is[1]) = 0.0 ------------------275------------------ Constraint equation to be differentiated: inverter.iAC[1] + aimc.is[1] - aimc.is[3] = 0.0 Differentiated equation: der(inverter.iAC[1]) + der(aimc.is[1]) - der(aimc.is[3]) = 0.0 ------------------268------------------ Constraint equation to be differentiated: 0.0 = inverter.iAC[2] + inverter.iAC[1] + inverter.iAC[3] + inductor.inductor[1].i + inductor.inductor[3].i + inductor.inductor[2].i Differentiated equation: 0.0 = der(inverter.iAC[2]) + der(inverter.iAC[1]) + der(inverter.iAC[3]) + der(inductor.inductor[1].i) + der(inductor.inductor[3].i) + der(inductor.inductor[2].i) Update Incidence Matrix: 215 190 189 178 193 192 187 186 270 169 168 167 89 271 88 272 87 207 213 214 212 208 206 273 274 275 268
From this it finds a static selection so i assume it is correct. Unfortunately shortly after initialization we have event shattering:
record SimulationResult
resultFile = "",
simulationOptions = "startTime = 0.0, stopTime = 1.5, numberOfIntervals = 30000, tolerance = 1e-06, method = 'dassl', fileNamePrefix = 'Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive', options = '', outputFormat = 'mat', variableFilter = '.*', cflags = '', simflags = ''",
messages = "Simulation execution failed for model: Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive
LOG_SUCCESS | info | The initialization finished successfully without homotopy method.
assert | debug | Simulation terminated due to too many, i.e. 20, event iterations.
| | | | This could either indicate an inconsistent system or an undersized limit of event iterations.
| | | | The limit of event iterations can be specified using the runtime flag '–mei=<value>'.
",
timeFrontend = 0.8346136749999999,
timeBackend = 0.78348839,
timeSimCode = 0.06675618500000001,
timeTemplates = 0.08867684899999995,
timeCompile = 1.288551428
end SimulationResult;
""
@Francesco Do you have any clue why this could happen? Is this index reduction what you would expect? (see full log in attached file)
follow-up: 43 comment:42 by , 6 years ago
Very good that you managed to identify the constraint on the six currents!
I compared the state selection with Dymola's: unfortunately, loadInertia.phi is missing, and I guess that is a problem, because it seems to me from a physical standpoint that one is free to select the initial angle of rotation of the load arbitrarily, so this state should not be removed. I don't see any other state that could take its place.
Can you please check why loadInertia.phi is removed from the candidates? As far as I understand, it shouldn't.
comment:43 by , 6 years ago
Replying to casella:
Can you please check why
loadInertia.phiis removed from the candidates? As far as I understand, it shouldn't.
loadTorque.phi is an alias of loadInertia.phi and therefore used. Since for index reduction only the highest order derivatives present in the equations, are state candidates and loadInertia.w occurs, it is not considered as a candidate. That just results in it being a continuous state rather than even being an option to become a dummy, which seems correct.
State Order: (9) ============= loadTorque.phi ---d/dt---> loadInertia.w loadInertia.w ---d/dt---> loadInertia.a aimc.airGapS.psi_mr[2] ---d/dt---> aimc.airGapS.spacePhasor_r.v_[2] aimc.airGapS.psi_mr[1] ---d/dt---> aimc.airGapS.spacePhasor_r.v_[1] aimc.airGapS.psi_ms[2] ---d/dt---> aimc.airGapS.spacePhasor_s.v_[2] aimc.airGapS.psi_ms[1] ---d/dt---> aimc.airGapS.spacePhasor_s.v_[1] aimc.strayLoad.phi ---d/dt---> aimc.strayLoad.w aimc.friction.phi ---d/dt---> aimc.friction.w aimc.phiMechanical ---d/dt---> aimc.wMechanical
Is loadInertia.a a state or algebraic? Right now it is not considered a candidate, but loadInertia.w is, if loadInertia.a was a state that would be incorrect.
follow-ups: 45 46 comment:44 by , 6 years ago
I made further investigation and it seems like there is no problem for the symbolic manipulations in general. My assumption is that we need another improvement to simulate this model.
The mentioned event shattering results from some events of which the zero-crossing thresholds are very close to each other. All of those events are time events, therefore there should not be any problem in simulating them in the correct order and without triggering each other. Some of those time events are treated as if they were state events, so the actual zero crossing has to be searched and that seems to trigger the other events causing shattering.
I will try to push my changes regarding the ASSC algorithm and furthermore try to remove the reshuffleLoops algorithm. ASSC should do the same manipulations and some additional tearing/causalization of linear integer subparts of algebraic loops which should result in better simulation time. Afterwards i will investigate this shattering problem further. We need to update the handling of those events and i assume that it will solve this particular problem.
comment:45 by , 6 years ago
Replying to Karim.Abdelhak:
I made further investigation and it seems like there is no problem for the symbolic manipulations in general. My assumption is that we need another improvement to simulate this model.
OK. Is there any way I can run this model myself with a nightly? Have you already committed the relevant code updates?
The mentioned event shattering results from some events of which the zero-crossing thresholds are very close to each other. All of those events are time events, therefore there should not be any problem in simulating them in the correct order and without triggering each other. Some of those time events are treated as if they were state events, so the actual zero crossing has to be searched and that seems to trigger the other events causing shattering.
This may be related to the issue with Modelica.Magnetic.FundamentalWave.Examples.BasicMachines.SMPM_Braking, that also fails because of too many event iterations.
BTW, #2152 asks to deal with time events more efficienty since 2012. Can we make some plant to implement this feature?
I will try to push my changes regarding the ASSC algorithm and furthermore try to remove the reshuffleLoops algorithm. ASSC should do the same manipulations and some additional tearing/causalization of linear integer subparts of algebraic loops which should result in better simulation time. Afterwards i will investigate this shattering problem further. We need to update the handling of those events and i assume that it will solve this particular problem.
OK, great!
comment:46 by , 6 years ago
Replying to Karim.Abdelhak:
The mentioned event chattering results from some events of which the zero-crossing thresholds are very close to each other. All of those events are time events, therefore there should not be any problem in simulating them in the correct order and without triggering each other. Some of those time events are treated as if they were state events, so the actual zero crossing has to be searched and that seems to trigger the other events causing shattering.
Karim has some good ideas about how to solve this issue, but that will need some implementation work.
follow-up: 51 comment:47 by , 6 years ago
| Resolution: | → fixed |
|---|---|
| Status: | assigned → closed |
It looks like the index reduction problem was solved long time ago. The model still has issues related to the PWM generator and event generation, see #5940
comment:48 by , 6 years ago
| Milestone: | 2.0.0 → 1.16.0 |
|---|
comment:49 by , 5 years ago
I was running into a singularity problem with another electric machine simulation example using a delta connected induction machine. However, I thus double checked the originally investigated model Modelica.Electrical.Machines.Examples.AsynchronousInductionMachines.AIMC_InverterDrive which is addressed at the very beginning of this ticket. Even though the status of this ticket is set to closed this simulation model does not work in the actual nightly build version of OMEdit. It fails with the following error message(s):
[1] Real der(aimc.is[3])(start=0, nominal=1) [2] Real der(aimc.is[1])(start=0, nominal=1) [3] Real aimc.lssigma.spacePhasor_b.v_[2](start=0, nominal=1) [4] Real aimc.lssigma.spacePhasor_b.v_[1](start=0, nominal=1) [5] Real inverter.dc_p.v(start=0, nominal=1) [6] Real inverter.diode_p.idealDiode[3].s(start=0, nominal=1) [7] Real inverter.transistor_p.idealGTOThyristor[3].s(start=0, nominal=1) [8] Real inverter.transistor_n.idealGTOThyristor[3].s(start=0, nominal=1) [9] Real rectifier.diode_n.idealDiode[2].s(start=0, nominal=1) [10] Real rectifier.diode_p.idealDiode[2].s(start=0, nominal=1) The initialization finished successfully without homotopy method. [11] Real rectifier.diode_p.idealDiode[1].s(start=0, nominal=1) [12] Real rectifier.diode_n.idealDiode[1].s(start=0, nominal=1) [13] Real rectifier.diode_n.idealDiode[3].s(start=0, nominal=1) [14] Real rectifier.diode_p.idealDiode[3].s(start=0, nominal=1) [15] Real inverter.transistor_n.idealGTOThyristor[1].s(start=0, nominal=1) [16] Real inverter.diode_n.idealDiode[1].s(start=0, nominal=1) [17] Real inverter.diode_p.idealDiode[1].s(start=0, nominal=1) [18] Real inverter.transistor_p.idealGTOThyristor[1].s(start=0, nominal=1) [19] Real inverter.diode_n.idealDiode[2].s(start=0, nominal=1) [20] Real inverter.transistor_p.idealGTOThyristor[2].s(start=0, nominal=1) Warning: maximal number of iteration reached but no root found [21] Real inverter.diode_p.idealDiode[2].s(start=0, nominal=1) [22] Real inverter.transistor_n.idealGTOThyristor[2].s(start=0, nominal=1) [23] Real inverter.diode_n.idealDiode[3].s(start=0, nominal=1) Simulation process failed. Exited with code 255. Warning: maximal number of iteration reached but no root found Warning: maximal number of iteration reached but no root found Warning: maximal number of iteration reached but no root found Error solving nonlinear system 833 at time 0.00962499 Error solving nonlinear system 833 at time 0.00962499 nonlinear system 833 fails: at t=0.00962499
The investigation was performed using
Connected to OpenModelica 1.16.0~dev-606-gfe9ee42 Connected to OMSimulator unknown-linux
comment:50 by , 5 years ago
| Resolution: | fixed |
|---|---|
| Status: | closed → reopened |
comment:51 by , 5 years ago
Replying to casella:
It looks like the index reduction problem was solved long time ago. The model still has issues related to the PWM generator and event generation, see #5940
OK, even though the remaining issue may be related with the PWM generation, there is still an issue with the index reduction of the attached model IMCD.mo.
by , 5 years ago
Delta connected induction machine example not simulating
comment:52 by , 5 years ago
Even though the error message suggests a that this is a linear system solver issue,
The default linear solver fails, the fallback solver with total pivoting is started at time 0.000000. That might raise performance issues, for more information use -lv LOG_LS. Matrix singular! Failed to solve linear system of equations (no. 187) at time 0.000000, system is singular for U[2, 2]. The default linear solver fails, the fallback solver with total pivoting is started at time 0.000000. That might raise performance issues, for more information use -lv LOG_LS. Matrix singular! Failed to solve linear system of equations (no. 517) at time 0.000000, system is singular for U[2, 2]. The default linear solver fails, the fallback solver with total pivoting is started at time 0.000000. That might raise performance issues, for more information use -lv LOG_LS. Matrix singular! The initialization finished successfully without homotopy method. Failed to solve linear system of equations (no. 517) at time 0.000000, system is singular for U[2, 2].
I suspect an index reduction problem. If I add "dummy" star connected resistances to the induction machine, the simulation model IMCD2.mo works just fine.

OMC 2.0.0 should run all the MSL correctly, so I'm marking this as a blocker.